You’d be wrong in thinking that only spheres are capable of rolling. Yes, spheres or circles are the most common fixed-width solids, and you’ve seen them as wheels, ball-bearings, axles, footballs, but here’s where geometry gets really interesting. There are other shapes that are capable of rolling as freely as spheres do. They’re called fixed-width or constant-width solids, and are extremely fun to look at because they roll around as freely as a sphere does. In fact, if you decide to slice right into them through the middle, no matter what angle you’d slice them at, your knife would travel the exact same distance every single time! Constant-width solids aren’t as rare as you’d think. If you’ve ever seen a gif of a rotary combustion engine, or if you’ve seen those really cool drill bits that make square-shaped holes, you’ve seen constant-width geometry in some form. Zac Eichelberger, a mechanical engineer and design enthusiast demonstrated FOUR of them at work in tandem. The Reuleaux Polygons set comes with four incredibly intriguing solids of the same width, machined out of solid copper. These polished solids comprise a sphere, a Reuleaux Triangle, a Reuleaux Pentagon, and a Reuleaux Heptagon. Precision-made to be the exact same width, these tabletop toys are baffling and at the same time enjoyable, as you roll them around your desk while marveling the absurdity and awesomeness of geometry the same way Leonardo Da Vinci did when he discovered constant-width solids in the 1500s, or Franz Reuleaux when he began exploring them and their applications in the 1800s. The Reuleaux Polygons Collection makes a great tabletop accessory for anyone who loves math, geometry, design, and engineering. The four polished solids make for a great anxiety-busting toy, even more so when you place a plane on top of them to see how they roll perfectly without any change in their width! Yeah, science! Zac Eichelberger This mathematical collection showcases the evolution of Reuleaux Polygons. The Reuleaux Polygons set comes with four intriguing solids of the same width, machined out of solid copper. These polished solids comprise a sphere, a Reuleaux Triangle, a Reuleaux Pentagon, and a Reuleaux Heptagon. They are unique geometric shapes that have constant width when measuring from the 2 tangent planes on each side of the shapes surface. Here is a Reuleaux Triangle rolling between two parallel planes. A real world demonstration. Unlike a circle where the point of zero rotation stays in the center point of the shape, Reuleaux Polygons have and oscillating point of zero rotation. This is due to the radius of curvature for each face having an arc of a circle larger than the shape itself. So the center of mass moves as it rolls unlike a circle that has a static center of mass relative to the top and bottom parallel planes, but how are the arcs formed? 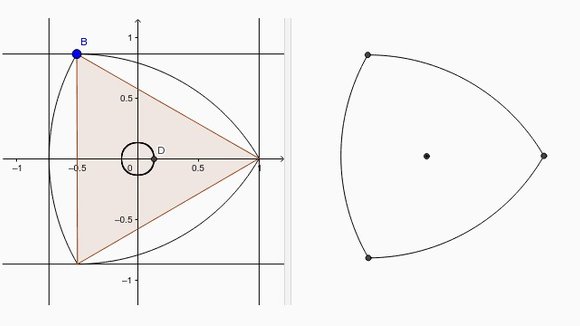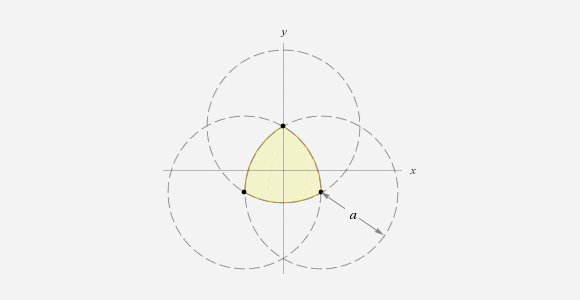An equilateral triangle inside of the Reuleaux Triangle provides the starting point for creating the perfect arcs to form a Solid of Constant Width. To make sure the intersecting points of each arc creates a perfect constant width around the object, the radius of each arc must be equal to the object’s width. As you see in the image, radius a on the intersecting circles is equal to the width of the yellow Reuleaux Triangle. Hurry, less than 24 hours left!